坦克車的前進
遇見三菱鏡
遇見凸透鏡
TRY it !
看完了前面的敘述與動畫,你是不是已經想到車子和折射之間的關係了?下面是一個關係對應表:
| 折射現象 | 類比 |
|---|---|
| 光 |  車子 車子 |
| 光疏介質 (如真空、空氣等) |  柏油路等可讓車子快速前進之硬地 柏油路等可讓車子快速前進之硬地 |
| 光密介質 (如水、玻璃等) |  沙地等會使車子前進速度變慢的軟地 沙地等會使車子前進速度變慢的軟地 |

我們為什麼一開始就先講車子的運動呢?其實,光在不同的介質中,也會以不同的速度前進。 例如,光在真空或是空氣中,它的速度就比在水中或是玻璃中快。
如果光線以斜向射入另一種介質中,就會因為速度不同,而產生偏向的結果,這就是造成折射的原因。
光在不同介質的傳播速率:
| 介質 | 光速(公里/秒) | 以c表示 |
|---|---|---|
| 空氣 | 300000 | c |
| 水 | 225000 | 3/4 c |
| 玻璃 | 200000 | 2/3 c |
看過了這個對照表,還有上面的動畫,我們可以回頭想想課本教過的一些概念:
如果我們在兩種介質交界面上的任何一點,作一條垂直於這個界面的直線(如左圖虛線),這條直線就是所謂的「法線」。如果你用剛才學的車子法則,分析光在不同介質裡的速度,決定折射的方向,你會發現結果剛好符合你在課本學過的一個規則:
「光由疏介質進入密介質,折射角偏向法線;光由密介質進入疏介質,折射角偏離法線。」
所謂的光疏或光密介質,其實是一個相對的概念,當兩種介質連在一起時,光前進比較快的就是疏介質,比較慢的是密介質,而不是絕對的。例如,如果一邊是空氣一邊是水,那麼空氣是疏介質,水是密介質;如果把水和玻璃放在一起,那水可能就成了疏介質,玻璃才是密介質。

所謂的光疏或光密介質,其實是一個相對的概念,當兩種介質連在一起時,光前進比較快的就是疏介質,比較慢的是密介質,而不是絕對的。例如,如果一邊是空氣一邊是水,那麼空氣是疏介質,水是密介質;如果把水和玻璃放在一起,那水可能就成了疏介質,玻璃才是密介質。
此外,這邊所謂的「偏向」某個方向,自然是和原本直線前進不偏折的方向做比較。而這個偏折通常不會太大,再怎麼大也絕對不會越過法線。
現在,你應該已經了解我們剛才為什麼要練習決定車子方向的原因了,如果你能利用「速度差」決定光折射的方向,就再也不必去背上面的規則了。
坦克的由來:從惠更斯原理、折射定律、到光學坦克車

在折射的單元中,我們使用坦克車作為折射現象的輔助說明工具。問題是,坦克車為什麼可以作為折射的類比呢?在 Halliday, Resnick, and Walker (1995) 的普通物理課本中,作者用了三、四頁的篇幅從惠更斯原理 (Huygens’ Principle) 推導出折射定律 (Law of Refraction 或是 Snell’s Law)。本單元的內容,並不是重述一遍課本的內容。目的之一,是幫助讀者了解坦克與光學折射之間的關係;目的之二,則是課本中這一段的公式推導,本身其實就是一段很精采的折射成因說明,覺得很適合物理老師、大學學生、或其他有興趣的人參考。
不論今天我們用什麼觀點解釋光學現象,至少在 Maxwell Equations 之前,這個原理對幾何光學的現象提出了很好的描述(這其實是一個很有趣的問題,希望將來有機會可以好好談談有關於「科學是什麼」的問題)。底下我們將看看,從惠更斯原理推導出折射定律的過程中,做了哪些假設及陳述;這些陳述和履帶坦克車在不同地面前進究竟有什麼相似之處,使我們可以借用坦克車作為折射現象的類比。推導過程所使用的數學應該不超過中學數學的範圍,想參考比較完整的敘述,請直接閱讀以上所提的大一普物課本,這裡只做個簡單的描述。
一、方程式推演
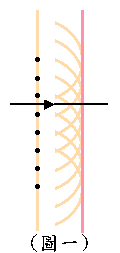 首先,惠更斯原理告訴我們說,在波前 (wavefront) 上的每一個點都可以視為一個點波源,產生新的球狀波(如圖一)。
首先,惠更斯原理告訴我們說,在波前 (wavefront) 上的每一個點都可以視為一個點波源,產生新的球狀波(如圖一)。
從這裡,我們可以發現一個平面波經過一段時間之後,所產生的新波前仍然是一個平面波。
剛才的平面波如果一直在同樣的介質〈如空氣〉中傳遞,它會一直平行前進;如果垂直進入另一種介質〈例如水或是玻璃〉,如我們所知,光前進的速度會改變。
現在我們考慮另一種狀況:如果這一束平行光以非垂直的方向進入另一種介質,情況會如何?(右圖)
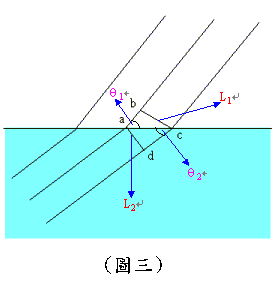 課本中畫了一個這樣的圖〈右圖三〉,然後怎麼開始計算呢?第一,我們知道,光在空氣中進行的速度比在水中快,所以,在同樣的時間內,光在空氣中前進的距離比在水中多。假設光在空氣中的速度是v1,在水中的速度是v2:
課本中畫了一個這樣的圖〈右圖三〉,然後怎麼開始計算呢?第一,我們知道,光在空氣中進行的速度比在水中快,所以,在同樣的時間內,光在空氣中前進的距離比在水中多。假設光在空氣中的速度是v1,在水中的速度是v2:
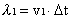
(方程式1)
我們剛說過,這兩個距離是在同樣的時間之內所走的,所以:
(方程式2)
從這裡我們先得到了前進距離和光速的關係。

上面的方程式告訴我們,一束平行光如果一直在同一個介質中前進,他會一直走下去;如果這一束平行光一邊走的快,一邊卻碰上了讓光走的比較慢的介質,那麼走得快的那邊會前進的比較多,而走得慢的那邊會前進的比較少。這個應該很容易想像。
接下來要討論的是,原本一起平行前進的光,一邊繼續前進,一邊速度減慢,會發生什麼事呢?假設 ac 之間的距離是 L:
在
這裡我們又知道了前進距離和入射角、折射角之間的關係〈至於這兩個角度為什麼剛剛好就是入射角和折射角,恐怕就得考考你兩個角度的定義及國中的三角學得怎樣了〉。接下來課本又考慮了折射係數和光速之間的關係,就導出了大家熟知的折射定律:
![]() 〈方程式 5〉
〈方程式 5〉
二、方程式分析
這裡我們省略了大部分的數學過程,只看每一段計算開始之前的敘述〈想知道詳細內容請參考課本〉。第一、從方程式1和2我們知道,光在不同介質中有不同的前進速度,所以相同時間內有不同的前進距離;第二、從方程式3和4我們又知道,由於一開始都是在同一平面直進的平行光,當一邊前進得多一邊前進得少,前進的方向就產生了不同的角度。所以從以上的兩點可知,這個角度的變化是由速度所決定的,而折射係數就是從光的速度定出來的,於是我們就得到了方程式中,折射係數和角度的關係。
三、坦克車與方程式

當我們了解了這一串方程式推導過程的關鍵之後,再來看看履帶坦克車。當坦克車在柏油路等硬地前進時,車子可以用全速前進;可是當坦克駛進沙地等軟泥地時,履帶會稍微打滑,不容易發揮車子真正的速度。所以在第一點提到的速度上,坦克車就相當於光,硬地則像是真空或是空氣等光疏介質,可以讓坦克以較快的速度前進;沙地像玻璃或水等光密介質,坦克前進速度較慢。如果坦克車以一個角度由硬地進入沙地,一邊履帶先進入沙地,慢了下來;另一邊還在硬地上快速前進,會出現什麼結果呢?當然就是會轉向。轉向哪個方向?一定是轉向比較慢的那邊,這個結果和方程式3、4計算的結果剛好是一樣的。等到坦克完全進入沙地之後,兩邊履帶以同速前進,又恢復直進。
如果我們只是定性地想由折射係數,也就是光在不同介質的傳播速度來決定光的偏轉方向,坦克車會是一個很好的類比,可以幫助學習者用推想的方式決定光偏折的方向。用速度差來推想折射方向,其結果和使用方程式5所得到的結果正好是一樣的。把這兩個結果用文字的方式定性地敘述出來,結果就是:
「光由疏介質進入密介質,折射角偏向法線;光由密介質進入疏介質,折射角偏離法線。」
 光向哪裡轉
光向哪裡轉 眼中的世界
眼中的世界 趣味實例
趣味實例 深度探討
深度探討
 下一個旅程:當光遇見三菱鏡
下一個旅程:當光遇見三菱鏡