參賽編號

20024

作品名稱

算計函數

適用年級

(可複選)

國中：■一年級 □二年級 □三年級

適用科目

數學

主題

函數及其圖形

預計教學時間

135分鐘

能力指標

（或教學目標）

7-a-12  能認識變數與函數。

7-a-13  能舉出例子，說明一次函數是一種特殊的比例對應關係。

7-a-14  能在直角座標平面上描繪一次函數的圖形。

＊能由對應值的表列來理解函數的對應關係。

＊能由數量間的數學關係理解函數關係。

＊能理解正比關係為函數關係。

＊能理解反比關係為函數關係。

＊能理解函數圖形的意義。

＊能在直角座標平面上描繪常數函數的圖形。

＊能在直角座標平面上描繪一次函數的圖形。

教材說明

 利用producer製作投影片影音教材，讓學生可以不受時空限制自我學習，並以二段有趣的影片(以鬼腳圖點出遊戲也能學數學以及怪怪計算機可以練習九九乘法的功能)引起學習動機，配合四張學習單能更有效學習，三張學習評量卷可以了解學習狀況，還有學習延伸單元提供給有興趣作加深加廣學習的同學。 

資料來源

九五年國中數學第二冊部編版。

高中數學第一冊—南一書局。

高中數學第一冊—三民書局。

生活的數學—九章出版社，羅浩源編著。

九一年國中數學第一冊國立編譯館。

主要教學活動

媒體與工具

電腦、Internet Explorer、Flash、Gsp、喇叭、Excel

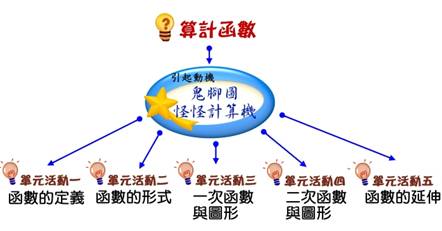
教學活動進行的步驟或流程

主題一：函數的定義

好玩的鬼腳圖遊戲：(看FLASH動畫)利用鬼腳圖引起動機，並   說明對應關係。

怪怪計算機：看小黃、小白如何利用計算機來學習九九乘法表，每輸入一個值即可計算出結果。

好熱的天氣：今年7/15氣溫觀測結果，觀察每一個觀測時間對應的溫度。

計程車車資問題：知道搭乘的里程數即可對應出車資。

函數的概念及定義：先說明前面四個例子的〝對應關係〞。對於任意給定的一個x值，都恰有一個y值與它對應，此時y是x的函數。表示成y = f(x)，即y is a function of x，唸成y等於f of x。

函數值：函數值y=f(x)指當x值確定時，y的值也唯一確定，則y就是f(x)。

主題二、函數的形式

函數的對應：

      一對一是函數

     多對一是函數

     一對多不是函數

     一對無不是函數

主題三、一次函數與圖形

 畫一次函數的圖形：取很多的數對，畫在直角座標平面上，可以看出一次函數圖形為一條直線。

 一次函數的形式：能寫成y=ax+b形式的函數，我們稱y為x的一次函數(a≠0)。

 常數函數及零函數。

 正比與反比的圖形。

主題四、二次函數與圖形

 畫二次函數的圖形：取很多的數對，畫在直角座標平面上，可以看出二次函數圖形為一條平滑曲線。

 拋物線：二次函數圖形即為拋物線。

主題五、函數的延伸

 函數的定義域與值域：包函所有x值的集合為定義域，包函所有y值的集合為值域。

 一直線判別函數：利用直線與函數圖形的交點數量來判斷函數。

作業評量

       學習單一、怪怪計算機            評量卷一

      學習單二、鬼腳圖                    評量卷二

      學習單三、認識函數                 評量卷三

      學習單四、一次函數                 flash線上擂臺