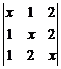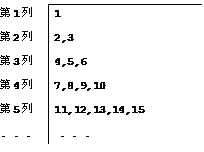八十九學年度大學入學考試中心學科能力測驗數學考科試題

第一部份: 選擇題

壹、單一選擇題：
說明：第1至7題，每題選出最適當的一個選項，標示在答案卡之「解答欄」，每題答對得5
             分，答錯不倒扣。

1.    

有一等腰三角形底邊為10，頂角72°。下列何者可以表示腰長？
(A)5×sin36°  (B)5×tan36°  (C)5×cot36°  (D)5×sec36°  (E)5×csc36°
                                                                                                              (2-2-3&2-2-5)

 

(E)

 

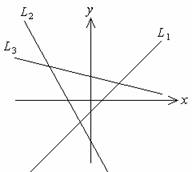
2.    

在坐標平面上，根據方程式x+5y-7=0, 2x+y+4=0, x-y-1=0畫出三條直線L1, L2, L3，如圖所示。試選出方程式與直線間正確的配置？

(A)L1: x+5y-7=0; L2: 2x+y+4=0; L3: x-y-1=0
(B)L1: x-y-1=0; L2: x+5y-7=0; L3: 2x+y+4=0
(C)L1: 2x+y+4=0; L2: x+5y-7=0; L3: x-y-1=0
(D)L1: x-y-1=0; L2: 2x+y+4=0; L3: x+5y-7=0
(E)L1: 2x+y+4=0; L2: x-y-1=0; L3: x+5y-7=0  (1-2-3)

 

(D)

 

3.    

下列5組資料(每組各有10筆)
A： 1, 1, 1, 1, 1,10,10,10,10,10
B： 1, 1, 1, 1, 1, 5, 5, 5, 5, 5
C： 4, 4, 4, 5, 5, 5, 5, 6, 6, 6
D： 1, 1, 2, 2, 3, 3, 4, 4, 5, 5
E： 1, 2, 3, 4, 5, 6, 7, 8, 9,10
試問哪一組資料的標準差最大？
(A)A   (B)B   (C)C   (D)D   (E)E   (4-3-7)

 

(A)

 

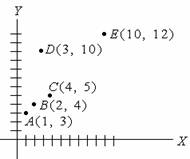
4.    

如圖所示有5筆(X,Y)資料。試問：去掉哪一筆資料後，剩下來4筆資料的相關係數最大？

(A)A   (B)B   (C)C   (D)D   (E)E   (5甲-1-4)

 

(D)

 

5.    

假設世界人口自1980年起，50年內每年增長率均固定。已知1987年世界人口達50億，1999年第60億人誕生在賽拉佛耶。根據這些資料推測2023年世界人口數最接近下列哪一個數？
(A) 75億  (B) 80億  (C) 86億  (D) 92億  (E) 100億     (1-3-1)

 

(C)

 

6.    

在1999年6月1日數學家利用超級電腦驗證出26972593-1是一個質數。若想要列印出此質數至少需要多少張A4紙？假定每張A4紙，可列印出3000個數字。在下列選項中，選出最接近的張數。[log102»0.3010]
(A) 50  (B) 100  (C) 200  (D) 500  (E) 700  (2-1-6)

 

(E)

 

7.    

設P1表示丟2個公正硬幣時，恰好出現1個正面的機率，P2表示擲2個均勻骰子，恰好出現1個偶數點的機率，P3表示丟4個公正硬幣時，恰好出現2個正面的機率。試問下列選項何者為真？
(A) P1=P2=P3  (B) P1=P2>P3  (C) P1=P3<P2  (D) P1=P3>P2
(E) P3>P2>P1 (4-3-2)

 

(B)

 

貳、多重選擇題：
說明：第8至10題，每題至少有一個選項是正確的，選出正確選項，標示在答案卡之「解答
             欄」。每題答對得5分，答錯不倒扣，未答者不給分。只錯一個可獲2.5分，錯兩個或
             兩個以上不給分。

8.    

在坐標平面上，以(-1, 1), (3, 1)為焦點，且通過點(3, 4)畫一雙曲線。試問此雙曲線也會通過下列哪些點？
(A)(1, 1)  (B)(-1, 4)  (C)(3, -2)  (D)(-1, -2)  (E)(3, 1)   (4-1-3)

 

(B)(C)(D)

 

9.    

阿山家在一條東西向馬路的北方D點處，為了不同目的，他走到馬路的路線有下列三條：
向南走a公尺到A點之後，繼續向南走a公尺到達馬路；
向東南走b公尺到B點之後，繼續向南走b公尺到達馬路；
向東走c公尺到C點之後，繼續向南走c公尺到達馬路。
根據上述資料，下列選項何者為真？
(A) c=2a
(B) a<b<c
(C) b=a
(D) A,B,C,D四點共圓
(E) A,B,C三點剛好在以D點為焦點的拋物線上     (4-1-1)

 

(A)(B)(E)

 

10.     

將行列式展開得到多項式f(x)。下列有關f(x)的敘述，何者為真？
(A) f(x)是一個三次多項式  (B) f(1)=0  (C) f(2)=0  (D) f(-3)=0
(E) f(5)=0  (3-3-2)

 

(A)(B)(C)(D)

 

第二部份: 填充題
說明：每題完全答對給5分，答錯不倒扣，未完全答對不給分。

A.  

今年(公元2000年是閏年)的1月1日是星期六。試問下一個1月1日也是星期六，發生在公元哪一年？     (1-2-1)

 

2005年

 

B.   

將自然數按下列規律排列，每一列比前一列多一個數，如下表所示：

試問第100列第3個數是多少？     (1-3-3)

 

4953

 

C.   

設三次方程式x3-17x2+32x-30=0有兩複數根a+i，1+bi，其中a，b是不為0的實數，試求它的實根。     (1-4-5&3-3-2)

 

15

 

D.  

空間中有一直線L與平面E:x+2y+3z=9垂直。試求通過點(2,-3,4)且與直線L垂直的平面方程式。     (3-2-4)

 

x+2y+3z-8=0

 

E.   

在某海防觀測站的東方12海浬處有A、B兩艘船相會之後，A船以每小時12海浬的速度往南航行，B船以每小時3海浬的速度向北航行。問幾小時後，觀測站及A、B兩船恰成一直角三角形?  (2-2-3)

 

2小時

 

F.   

氣象局測出在20小時期間，颱風中心的位置由恆春東南方400公里直線移動到恆春南15°西的200公里處，試求颱風移動的平均速度。(整數以下，四捨五入) (2-2-6)

 

17公里/小時

 

G.   

桌面上有大小兩顆球，相互靠在一起。已知大球的半徑為20公分，小球半徑5公分。試求這兩顆球分別與桌面相接觸的兩點之間的距離。
     (3-4-4)

 

20公分

 

H.  

體操委員會由10位女性委員與5位男性委員組成。委員會要由6位委員組團出國考察，如以性別做分層，並在各層依比例隨機抽樣，試問此考察團共有多少種組成方式?  (4-2-4)

 

2100種

 

I.     

交通規則測驗時，答對有兩種可能，一種是會做而答對，一種是不會做但猜對。已知小華練習交通規則筆試測驗，會做的機率是0.8。現有一題5選1的交通規則選擇題，設小華會做就答對，不會做就亂猜。已知此題小華答對，試問在此條件之下，此題小華是因會做而答對(不是亂猜)的機率是多少？     (5甲-1-1)

 

 

J.    

如下圖所示，有一船位於甲港口的東方27公里北方8公里A處，直朝位於港口的東方2公里北方3公里B處的航標駛去，到達航標後即修正航向以便直線駛入港口。試問船在航標處的航向修正應該向左轉多少度？(整數以下，四捨五入)
                                                                                                                 (2-2-6)

 

45度

 

參考公式及可能用到的數值

1. 一元二次方程式的公式解：x=

2. 通過(x1, y1)與(x2, y2)的直線斜率 m=

3. 等比數列<arn-1>的前n項之和Sn=, r¹1

4. DABC的正弦及餘弦定理
=2R, R為外接圓的半徑 (正弦定理)
‚c2=a2+b2-2abcosc (餘弦定理)

5. 統計公式：
算術平均數 M(=)=(x1+x2+…+xn)=
標  準  差 S=
相關係數   r=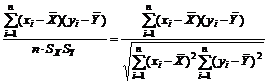
其中SX為變量X之標準, SY為變量Y之標準

6. 貝氏定理
P(A|B)=

7. 參考數值：

8. 對數值：