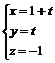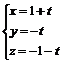|
1.
/ |
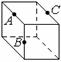
�p�k�Ϫ��|���@�i�}�ϡA�|���@���������2������ΡA�|�Ӱ������O�y����4�����y�T���ΡA�h���|���@������______
|
|
|
|
|
|||
|
2.
|
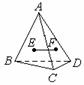
�N�@�ӥ��|���骺�|�ӭ��W���U�䤤�I�νu�q�s���A�i�o�|�Ӥp���|����Τ@�ӥ��K����A�p�U�ϩҥܡC�p�G��|����ABCD����n��12�A�����K���骺��n��______
|
|
|
|
|
|||
|
3.
|
�Ϥ@���@���ߤ���,
A, B, C���O���Ҧb���䤧���I, �q�LA,
B, C�T�I�������P���ߤ�������ۺI, �ݤU�C��̬���I�����Ϊ�? |
|
|
|
|
|||
|
4.
|
�����餤, �����n�u���W�u�@��______��. (87�Ǵ�) |
|
|
|
|
|||
|
5.
|
�Ҽ{�@���ߤ��餻�ӭ����U�����I, �h�H�䤤�|�Ӥ����I�����I������Τ@�@���X��? (1)3 (2)4 (3)6 (4)8 (5)12 (86�Ǵ�) |
|
|
|
|
|||
|
6.
|
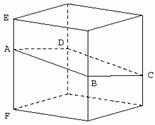
�Ǯջ\�F�@�ɥ��|���骺�����ū�(�p�U��). �����N�@���W��[�b�Ǥ�,
�@���Q�᪺���. ���ݤ��O�T�w�b�⭱��ABC�MACD������E, F�B. �ͪ��Ѯv�n�����D�o�ӿ��W�h��, �~��Фu�H�s�@. ���M |
|
|
|
|
|||
|
7.
|
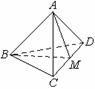
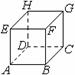
�U�Ϥ�ABCD�����|����, M�� |
|
|
|
|
|||
|
8.
|
�U�C�����Ŷ����ԭz,
���ǬO���T��? |
|
|
|
|
|
1.
|
�b�Ŷ���, �s���IP(2, 1, 3)�P�IQ(4, 5, 5)���u�q |
|
|
|
|
|||
|
2.
|
�b�Ŷ����Ф�, �]xy�������@�譱, ���@���u�q�L�IP(1, 2, 1), �g�V�譱�W���IO(0, 0, 0), �g�譱�Ϯg��q�L�IR. �Y |
|
|
|
|
|
1.
|
�U�Ϭ��@���ߤ���A �Q�@�����I�X�@�ӥ|���ABCD�A�䤤B, D���O���W�����I�A�B |
|
|
|
|
|||
|
2.
|
�ϤG���@���ߤ���,
�հݤU�C�̬��u? |
|
|
|
|
|||
|
3.
|
�b�Ŷ���, �U�C�����I�i�PA(1, 2, 3), B(2, 5, 3), C(2, 6, 4)�T�I�c���@����|��� (87�Ǵ�) |
|
|
|
|
|||
|
4.
|
���@���ߤ���, ��������O1, �p�G�V�q |
|
|
|
|
|
1.
|
�Ŷ������@���uL�P����E:x+2y+3z=9�����C�ըD�q�L�I(2,-3,4)�B�P���uL������������{���C (89�Ǵ�) |
|
|
|
|
|||
|
2.
|
�b�Ŷ���, �s���IP(2, 1, 3)�P�IQ(4, 5, 5)���u�q |
|
|
|
|
|||
|
3.
|
�]P�BQ������ax+by+cz=5�W��۲��I,�B |
|
|
|
|
|||
|
4.
|
�]q���⥭��2x-y+2z=6�P3x-4z=2������(���U��), �hq�̪�ƫƬ�_______�� (86�Ǵ�) |
|
|
|
|
|||
|
5.
|
�w�����uL1�BL2���(1, 0, -1), �B�ۤ�����, �䤤L1: |
|
|
|
|
|
1.
|
�]���uL����{���� |
|
|
|
|
|||
|
2.
|
�]L��x-y+z=1�Px+y-z=1�⥭������u, �h���uL�W�P�I(1, 2, 3)�Z���̪��I�����Ь�______ (83�Ǵ�) |
|
|
|
|