圓錐曲線源起
在希臘數學中，有三個眾所皆知的問題，它們被稱為「化圓為方」、「倍立方」、「三等分任意角」。化圓為方的意思是作一個正方形，其面積與一給定圓的面積相等。倍立方，就是構造一個立方體，其體積是已給定立方體體積的兩倍。三等分任意角，就是將任意一個角分為相等的三部分。這些作圓問題，限於僅僅使用一把直尺(沒有刻度，僅供為畫直線用)，一隻圓規，不允許使用任何其他的工具。這些對於作圖工具的限制，表明了古希臘人對待數學的態度，而直尺和圓規都是直線和圓的對應物。整體來說，希臘人在研究幾何上，會有這種非理性的限制，目的是為了保持幾何學的簡單、和諧，以及由此產生的美學魅力。
因此，以柏拉圖為代表的希臘學者，認為引入複雜的工具來解決古希臘的作圖問題，雖對手工繪製是可取，但對於一個思想家來說則是不足稱道，柏拉圖更認為，利用複雜的工具，那麼「幾何學的優點」就會盪然無存，因為這樣的話，我們又重新使幾何學退到了感性世界，而不是用思想中永恆的、超越物質的思維想像力去提高、充實它。
對於圓錐曲線的研究起源，一種說法是，解倍立方問題
(以尺規作)，可能是整個發展的起點。Hippocrates(公元前5世紀)認為若能做出連續比例中項
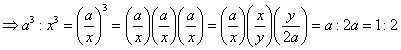
( 其中x代表2的立方根)。
因此，由這件事來解決倍立方問題，用現在我們熟悉的想法來說就是找出x2
= ax 與y2
= 2ax這兩個拋物線的交點。不過！要用尺規作圖來做拋物線是不可能做到的。
但在探討許多尺規作圖的過程中，數學家常有其他的發現。例如約西元前4世紀的Menaechmus就對圓錐曲線十分感興趣，他認為拋物線雖然無法以尺規作出，不過利用直線與圓，藉由比例，可以作出拋物線上的某些點，至少可以大致描繪出它的圖形。
他的理論基礎即以底下將長方形化成正方形的作圖出發，現在圖解如下：
由圖一x、y、z的關係知：x2 = yz
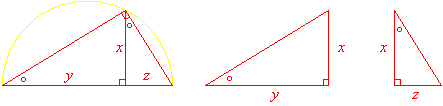
圖一
圖二，即是利用此原理，作一正方形，使其面積等於一長寬分別為a，b的矩形面積的簡易圖解：
圖二
圖(三)即可描繪出y2 = ax的大致圖形。
圖三
大體而言，圓錐曲線研究是由Euclid(公元前4世紀)，Apollonius(－287~－221)以圓錐被一平面從不同的角度所截來看待，方開始蓬勃發展。現在我們以代數方式來學習圓錐曲線，似乎極為自然，但對於古希臘幾何學而言，也不陌生，例如Euclid稱一個直角三角形以一股為軸旋轉，斜邊轉出而成的曲面叫圓錐，用平面以不同的角度來切割，即可切出三種不同的截痕。
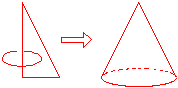
而現在所用的名稱如：
hyperbola(雙曲線)、parabola(拋物線)以及ellipse(橢圓) 此三字是Apollonius延續Euclid的觀點所使用的。從字母表面根本看不出個玄虛，若單從一般從字典，亦只能發現Hyper-表「超過」、「多」之意；para-表「平行」之意；而ellipsis為「省略」之意。事實上，Apollonius對圓錐曲線所提出hyperbola(雙曲線)、parabola(拋物線)以及ellipse(橢圓)這三個字，是謂「超過」、「重合」或「短於」的三個意思，說得更朋白一些hyperbole、parabole及ellipsis，就是more、equal及less之意。
由上面四個圖，可以看到：
(1) 當一截平面與傾斜超過(more than)圓錐的傾斜角θ其截面為雙曲線，如圖一。
(2) 當一截平面與傾斜等於(equal to)圓錐的傾斜角θ其截面為拋物線，如圖二。
(3) 當一截平面與傾斜少於(less than)圓錐的傾斜角θ其截面為橢圓，如圖三。