二   次   函   數

線型函數    二次函數    相關步驟    相關性質

線型函數  y=ax+b的圖形是一直線

    (1) a≠0時，y=ax+b叫做一次函數，其圖形是斜直線。

    (2) a=0時，y=b叫做常數函數，其圖形是平行於x軸的直線或y軸。

Ex、    y=2x 是一次函數，y=3是常數函數

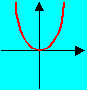
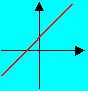
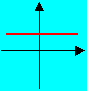
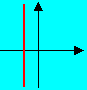
        試回答：    下列圖形何者為一次函數的圖形？何者為常數函數的圖形？

                (1)      (2)    (3)     (4)

　

                                                                   答：(2)--- 是一次函數    (3)--- 是常數函數

回到頁首

二次函數    y= f(x)= ax2+bx+c，其中a、b、c為常數且a≠0。

                          二次函數的圖形是拋物線

        

        試回答：

                下列哪些是二次函數？

                (1) f(x)=x2+x+1        (2) f(x)=2x     (3) f(x)= -0.5x2+1

　

                                                                    答：二次函數是  (1)、(3)

回到頁首

描圖步驟

    在座標平面上，畫出函數y=x2的圖形：

        第一步驟：選擇x值，然後求出對應的y值：

                            選x=…、-4、-3、-2、-1、0、1、2、3、4、…

                            分別代入y=x2中求值，並列表如下：

           

        第二步驟：將每一個數對所對應的點描到座標平面上。

        第三步驟：以平滑曲線將這些點連接起來。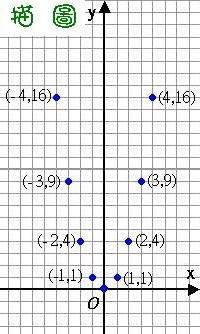

       

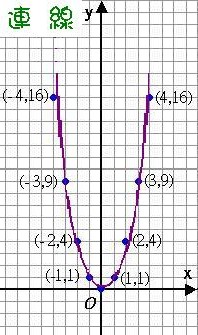
回到頁首

相關性質

 對稱軸：y=x2 的圖形中，沿著y軸把圖形對摺，恰好會處處疊合。
                 換句話說，它是以y軸為對稱軸的線對稱圖形。
           ● 問題來啦→有沒有對稱軸是x=3的二次函數？
  頂點：y=x2 的圖形有一個最低點(0，0)，也稱為此圖形的頂點。
             ● 問題來啦→是不是所有的頂點都是最低點？
  開口方向 ：y=x2 的圖形可以無限向上延伸，但不會相交
                       在一點，因此開口方向是向上的。
            ● 問題來啦→是不是所有的圖形 開口都是向上的？
  圖形移動：y=x2 的圖形向左平移2單位，即可得到y=(x+2)2
          ● 問題來啦→y=x2 的圖形要怎樣移動才能到達y=x2+2的圖形？

回到頁首